Natural Arch Dimensions

Introduction

It is desirable to determine the dimensions of natural arches for several reasons. For example, dimension measurements are useful for comparison, description, classification, and analysis.

Through comparison we answer questions such as which arch is longest, thinnest, tallest, etc. These questions are asked for a given region, geology, arch type, etc. Description is useful for selecting arches to visit or study, e.g., visiting only those arches larger than a given size, or studying a sample falling within some size range. Classification of arches into different size groups is a useful way to accomplish this. Also, it may be possible to base a morphological classification scheme on dimension measurements. (Note that the standard taxonomy presented on this site is a genetic scheme rather than morphological.) Finally, dimension measurements can be merged with other observable arch attributes to perform various analyses. For example, analysis of natural arch formation modes and evolutionary lifecycles require such data.

For dimension measurements to be useful in satisfying these purposes, they must be repeatable for any given arch and comparable for different arches. By repeatable, we mean that two different investigators will measure the same quantities when documenting an arch and, therefore, obtain similar or identical results. By comparable, we mean that any size comparison of two different arches will be based on measurements of the same spatial attributes.

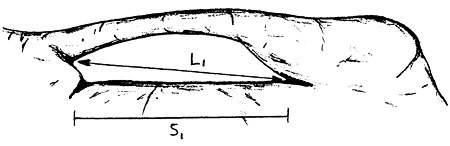
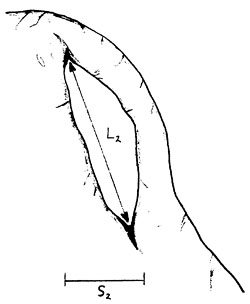
As an example of this, examine the two arches shown in Figure 1 below.

Figure 1a

Figure 1b

Different shapes or orientations can result in different interpretations of dimensions. For the two arches in Figure 1 above, L1 equals L2, while S1 is much greater than S2. Which of the two arches is "longer"?

If one investigator equates the length of an arch to a measurement of L while another equates it to a measurement of S, no matter how accurately they measure they will report different "lengths." Similarly, one investigator will say the two arches are about the same length while the other will say one arch is much longer than the other. The problem illustrated by this example becomes much more severe when dealing with the full range of morphological complexity exhibited by natural arches.

The solution to this problem is a set of universally accepted definitions for natural arch dimensions. Unfortunately, most of the dimension definitions found elsewhere, including those in the references, are vague at best, containing ambiguous terms and phrases. These ambiguities make repeatability and comparability difficult, if not impossible.

The set of dimension definitions below have been rigorously crafted to avoid ambiguity. They are applicable to all natural arch types. This standard set of dimensions, if carefully measured and recorded by all field observers, will enable repeatability and comparability and will thus permit the goals of comparison, description, classification, and analysis to be achieved.

Caveats

The definitions presented here are intended for use in describing and measuring any type of natural arch with a single opening. While these definitions can be successfully applied to many arches with multiple openings, in some such cases their use is problematic.

All of the dimensions defined here are linear extents of some part or component of an arch. Areas and volumes of various parts of arches might be useful to describe the spatial characteristics of arches, but are typically impossible to measure or even estimate in the field. For this reason, they are only discussed when doing so helps define a linear dimension of interest. While linear dimensions are also often difficult to measure, they are much more obtainable than areas or volumes.

This site does not discuss the several techniques by which arch dimensions can be measured. It tries to define which spatial extents should be measured, and from what point to what point the measurement should be made, but does not discuss how the measurement is actually taken, e.g. with a steel tape, or transit, or by visual comparison. Obviously, the accuracy of measurements obtained is dependent upon that choice.

Preliminaries

Before examining the definitions for natural arch dimensions, the reader should become familiar with two topics. First, the reader should review the meaning of some mathematical terms whose use is necessary to ensure the rigor of the dimension definitions. These terms are reviewed at Basic Terminology. Second, the reader should review the standard definitions for the basic components or parts of natural arches. These definitions are presented at Natural Arch Components.

Morphology Independent Dimensions

Some dimensions are applicable to natural arches of any shape, while others only have meaning if the arch's shape is of a certain type. For example, the "vertical thickness of the lintel" has little meaning for a pillar arch. Thus, there are dimensions that do not depend on the morphology of the arch, and there are dimensions that are morphology dependent. This section defines some morphology independent dimensions.

Perhaps the most commonly used dimension existing in the literature today is a natural arch's span. In reference 1, Vreeland defines the span of a natural arch to be "the maximum horizontal length of the opening between supports, measured where the full opening is at its minimum," and "the horizontal length of the unsupported rock." There are two ambiguities in these definitions. It is not clear what is meant by the phrase "where the full opening is at its minimum," nor is it obvious in all cases which parts of the rock are supported and which are unsupported.

This ambiguity can be removed by recasting Vreeland's definition using the terms described in Basic Terminology. The new, rigorous definition for the span of a natural arch is the min/max of the lengths of the horizontal projections of the chords of all opening orbits. In other words, consider all the opening orbits on the arch's surface. On each one, draw all possible chords and project them onto the horizontal. For each opening orbit, select the longest of these projections. This is just the maximum horizontal extent of the orbit. From this set of longest projections, one for each opening orbit, select the shortest. This is just the shortest maximum horizontal extent of any opening orbit. The length of the selected projection is the span. It corresponds to S in Figure 1.

Note that the span was defined as a scalar value, i.e., a length. It is useful also to determine the orientation of the projection that was selected by the min/max operator. Obviously, this projection is confined to the horizontal, but its azimuth is arbitrary. Therefore, another important attribute of the arch which should be measured is the orientation, or azimuthal angle, of the projection whose length is the span.

It is possible that more than one projection will produce the same min/max length we call the span. These projections might be associated with completely different orbits and hence have different azimuths. For example, this would be true for a hypothetical arch shaped like a pipe with a bend in the middle. Of course, natural arches seldom exhibit this degree of symmetry. In practice the projection which produces the span will be unique and the azimuth will also be unique.

Another dimension which is useful to cast in the min/max notation is the length of light opening defined by Stevens and McCarrick in reference 2. The new, rigorous definition is the min/max of the lengths of the chords of all opening orbits. This corresponds to L in Figure 1. As with the span, it is useful also to determine the azimuthal angle of the chord which produces the length of light opening. Furthermore, since this chord is not confined to the horizontal, the angle the chord makes with the vertical should also be determined.

Analogs to the span and length of light opening exist for the lintel. These dimensions use lintel orbits rather than opening orbits. Thus, the min/max of the lengths of the horizontal projections of the chords of all lintel orbits is a recast, rigorous definition for both Vreeland's width (reference 1) and Stevens/McCarrick's horizontal thickness (reference 2).

The other analog, the min/max of the lengths of the chords of all lintel orbits, does not correspond to any currently published dimension, but seems to be a useful one, especially for vertically oriented lintels. We call this new dimension the lintel breadth.

At this point, we have defined four primary dimensions: span, length of light opening, width, and lintel breadth. We now define dimensions that are orthogonal (perpendicular) to the orientations of these primary dimensions. Two of these orthogonal dimensions apply to any arch and are defined next. Others apply only to certain well-defined morphological classes of arches and are therefore defined in the next section.

The Stevens/McCarrick dimension called depth of light opening (reference 2) can be defined as the min/max of the lengths of the opening orbit chords orthogonal to the length of light opening chord. Similarly, we define the lintel depth to be the min/max of the lengths of the lintel orbit chords orthogonal to the lintel breadth chord. These two definitions complete our set of morphology independent arch dimensions.

Morphology Dependent Dimensions

The dependence on arch morphology for our dimension definitions is minimized by dividing all arches into classes based upon three characteristics that are easily determined for any arch shape. Arches that do not have any vertical opening orbits must be treated as special cases. This is also true for arches that don't have any vertical lintel orbits. Finally, arches that have horizontal opening orbits should be treated differently from arches that do not.

For arches with vertical opening orbits, Vreeland's height (reference 1) is redefined as the min/max of the lengths of the vertical projections of the chord of all vertical opening orbits. For arches without vertical opening orbits, Vreeland's height is redefined as the length of a vertical line segment drawn down to the ground from the min/max of the elevations of all points on all opening orbits.

For arches with vertical lintel orbits, both thickness (reference 1) and vertical thickness (reference 2) are redefined as the min/max of the lengths of the vertical projections of the chords of all vertical lintel orbits. For arches without vertical lintel orbits, we artificially create an analog to them by considering the volume of rock above the opening to be detached and suspended in air. This volume must have vertical orbits. These are analogous to vertical lintel orbits, but aren't constrained to the arch surface. Rather they are constrained to the surface of the volume of rock above the opening considered in isolation. Using this construct, thickness and vertical thickness are redefined as the min/max of the lengths of the vertical projections of the chords of all vertical orbits of the volume of rock above the opening.

For arches with horizontal opening orbits, Vreeland's width of opening (reference 1) is redefined as the min/max of the lengths of the horizontal opening orbit chords orthogonal to the span projection. For arches without horizontal opening orbits, Vreeland's width of opening is not applicable. In some of these cases, either the separation dimension or the divergence dimension is of interest. These two dimensions are defined next.

Some arches are adjacent to a cliff wall that provides no support to any part of the lintel, but which noticeably occludes the opening. Two obvious examples are Black Arch and Surprise Arch in Arches National Park. In such cases, the separation of the arch from the occluding cliff wall is of interest. This separation is defined as the minimum distance found between any of the set of points on all planar lintel orbits and any of the set of points on the cliff wall surface. Note that if this minimum distance is zero, then the cliff wall is providing some support to the lintel and this dimension is not applicable. In this case, either use width of opening if the arch has horizontal opening orbits or divergence if it does not.

Some arches are adjacent to a cliff wall which provides some support to the span and occludes the opening, but the arch still has no horizontal opening orbits. An example of this is Mesa Arch in Canyonlands National Park. In cases like this, the separation dimension defined above will be zero. What remains of interest, however, is the maximum divergence of the lintel from the cliff wall. For this particular morphology, divergence is defined as the maximum distance found along a straight line segment orthogonal to the span projection between any of the set of points on all planar lintel orbits and any of the set of points on the cliff wall surface. Note that the restriction of measuring orthogonal to the span projection does not restrict the divergence dimension to be horizontal. Although the divergence will be horizontal for many arches, in some cases it will not be. The divergence of Mesa Arch, for example, is not horizontal because the span extends above the top of the adjacent cliff wall.

Refinement of Semantics

Various authors use different words to label the natural arch dimensions they have defined. Looking across the literature, the reader will find many examples of the same word meaning different things and the same dimension labeled with different words. For this reason, we have chosen to modify some of the semantics used by these authors and recast the definitions of the standard set of dimensions using a standardized set of dimension labels. This standardized semantics for dimensions is based on the following analysis.

A popular dictionary contains the following definitions:

• length – the greatest of the two or three dimensions of anything
• span – the distance between two ends or supports; as, the span of an arch
• width – distance from side to side
• breadth – measure of anything from side to side; width
• height – the distance from the bottom to the top
• thickness – dimension from surface to opposite surface
• depth – the distance from the top straight downward, from the surface or edge inward, or from front to back

Several conclusions are drawn from these:

• Length is a poor choice for labeling arch dimensions because it implies the longest (greatest) dimension. The definitions that currently include length in their name are not always the longest dimension for all morphologies. Indeed, no dimension can be consistently applied for all arch morphologies and always be the longest dimension.
• Span is a good choice for labeling the dimension Vreeland calls span. Indeed, span is used throughout the general literature on arches in ways similar to the meaning Vreeland intends. It seems unnecessary and even inappropriate to replace it.
• Width is a good choice for labeling arch dimensions as long as we have a common understanding of what "side to side" means for arches. What seems natural is to use width to label horizontal dimensions.
• Breadth, like width, is a good choice. However, since its dictionary definition is identical with width, is there a need for it? Since we used width to label horizontal dimensions, we use breadth to label dimensions that are "from side to side" but are not necessarily horizontal.
• Height is a good choice and seems to be used correctly and consistently by most authors.
• Thickness is a good choice. Although no orientation is implied by the definition, both references 1 and 2 use it to label vertical dimensions. Unfortunately, reference 2 also uses it for a horizontal dimension. Since thickness is often paired with width in common usage, we constrain its use to vertical dimensions orthogonal to width.
• Depth is a good choice. Since it is often paired with breadth, we use it for dimensions orthogonal to those described using breadth.

All but two of the terms used to label dimensions in reference 1 and 2 are consistent with the above. To remove those exceptions, we have renamed length of light opening from reference 2 to opening breadth. Similarly, horizontal thickness from reference 2 has been changed to width. These changes are reflected in the synopsis of dimension definitions below.

Dimension Definition Synopsis

The following are rigorous definitions for the standard set of natural arch dimensions that should be measured and reported when documenting a natural arch. These dimensions are divided into two subsets. The first contains dimensions which are aligned with the vertical as a reference direction. These are called aligned dimensions. The second contains dimensions which are not tied to the vertical. These are called unaligned dimensions. Both subsets are further divided into dimensions pertaining to the opening and dimensions pertaining to the lintel.

Aligned Dimensions for the Opening:

• SPAN - the min/max of the lengths of the horizontal projections of the chords of all opening orbits.
  
  
• HEIGHT - the min/max of the lengths of the vertical projections of the chords of all vertical opening orbits; if there are no vertical opening orbits, then the length of a vertical line segment drawn down to the ground from the min/max of the elevations of all points on all opening orbits.
  
  
• WIDTH OF OPENING - the min/max of the lengths of the horizontal opening orbit chords orthogonal to the span projection; if there are no horizontal opening orbits, then this dimension is not applicable.
  
  
• SEPARATION - the minimum distance found between any of the set of points on all planar lintel orbits and any of the set of points on an adjacent cliff wall surface; only applicable if there are no horizontal opening orbits.
  
  
• DIVERGENCE - the maximum distance found along a straight line segment orthogonal to the span projection between any of the set of points on all planar lintel orbits and any of the set of points on an adjacent cliff wall surface; only applicable if there are no horizontal opening orbits and the separation is zero.

Aligned Dimensions for the Lintel:

• WIDTH - the min/max of the lengths of the horizontal projections of the chords of all lintel orbits.
  
  
• THICKNESS - the min/max of the lengths of the vertical projections of the chords of all vertical lintel orbits; if there are no vertical lintel orbits, then the min/max of the lengths of the vertical projections of the chords of all vertical orbits of the volume of rock above the opening volume.

Unaligned Dimensions for the Opening:

• OPENING BREADTH - the min/max of the lengths of the chords of all opening orbits.
  
  
• OPENING DEPTH - the min/max of the lengths of the opening orbit chords that are orthogonal to the opening breadth chord.

Unaligned Dimensions for the Lintel:

• LINTEL BREADTH - the min/max of the lengths of the chords of all lintel orbits.
  
  
• LINTEL DEPTH - the min/max of the lengths of the lintel orbit chords that are orthogonal to the lintel breadth chord.

Discussion

The dimensions defined above fall into groups. This is no accident since they are all either directly based on, or natural extensions of, the groups of dimensions found in references 1 and 2. Vreeland's span and height are an orthogonal pair aligned with the vertical. As such, the pair attempts to characterize the arch's defiance of gravity. This intent is reflected in Vreeland's use of the phrase "the horizontal length of the unsupported rock" in his definition of span. A set of dimensions aligned with the vertical provides valuable information on both the appearance of the arch and its structural character.

When Vreeland's width of opening dimension is applicable, it is orthogonal to both the span and the height, creating a three-dimensional set. When width of opening is not applicable, one of three cases obtains, depending on whether or not the arch is next to a cliff wall. For two of these three cases, new dimensions have been defined to complement span and height. For the last case, no third dimension is needed.

First, if there is an adjacent cliff wall that occludes the arch opening but provides no support to the lintel, then the separation dimension replaces width of opening as the third member of the trio. Second, if the occluding cliff wall does provide support to the lintel, then the divergence should be measured as the third dimension. The divergence will be orthogonal to the span, but may or may not be orthogonal to the height. Lastly, if there is no adjacent cliff wall, then no third dimension is needed. For example, there is no reason to measure the distance from Delicate Arch to the nearest projecting rock mass, since this has no effect on the structure or appearance of the arch.

The alternative opening dimensions used by Stevens and McCarrick, labeled opening breadth and opening depth in the Synopsis above, are not aligned with the vertical. Rather they are free to conform to the orientation of the arch. They do form an orthogonal pair. These dimensions provide valuable information on the overall size of the arch opening regardless of its orientation. They also complement the Vreeland opening dimensions. In fact, a comparison of span and height to opening breadth and opening depth can provide an indication of the gross shape and orientation of the opening.

Vreeland's width and thickness dimensions for the lintel are also an orthogonal pair aligned with the vertical. The Stevens and McCarrick lintel dimensions, horizontal and vertical thickness, are identical to width and thickness respectively.

The newly defined lintel breadth and lintel depth are an orthogonal pair that are not aligned with the vertical and are free to conform to the orientation of the arch. They are an obvious extension of the opening breadth and opening depth. As with those opening dimensions, this unaligned pair nicely complements the vertically aligned pair to grossly characterize the fragility, size, and orientation of the lintel.

In addition to the standard set defined above, there are many other possible natural arch dimensions that could be defined. Two that are found in references 1 and 2 respectively are total height and extent, but the list is endless. Some can be defined using the same rigorous methods employed for the standard set. For example, total height could be defined as the difference between the maximum elevation of any point in the lintel and the minimum elevation of any point in the opening. Others probably are not definable using this method, for example extent.

The dimensions included in the standard set were selected for the following reasons. First and foremost, they are now rigorously defined and hence can be applied repeatably. They are also generically defined so that they can be applied to any arch and hence permit comparability between different arches. Finally, they are based on, or are obvious extensions of, already published dimensions that are in common use. It is important to note that the standard set implies a minimum set of dimensions to be measured to document an arch. Nothing prevents an investigator from including measurements of other dimensions in an arch's documentation. Should this be done, however, it is hoped that they will be well defined.