Basic Terminology

The dimension definitions for natural arches presented in these pages make extensive use of a few basic mathematical terms, especially certain concepts from the discipline of topology. Doing so avoids ambiguity. Since these mathematical terms have explicit and rigorous meanings, they make the definitions concise, albeit somewhat dense for many non-technical readers. Any attempt to maintain rigor without their use would require excessively lengthy and clumsy definitions. Therefore, it is necessary to define the basic set of mathematical terms that are routinely used throughout these definitions. Readers who wish to measure natural arches in accordance with the set of standard dimensions presented here must have an appreciation of these concepts.

Surfaces, Points, Curves, and Chords

As a start, some readers may wish to review the following basic mathematical terms: point, line, curve, and surface. In order to define some additional, more complex terms, we will be working with points and curves drawn on two-dimensional surfaces that are curved in three-dimensional space.

It is also important for the reader to understand the difference between a closed curve and an open curve. Similarly for surfaces, a closed surface bounds a volume while an open surface does not. Thus, a balloon and an inner tube are both closed since they bound the volume of air inside them. On the other hand, a sheet of paper bounds no volume. It does not make sense to talk about the volume of air "inside" the sheet of paper. It is an open surface.

Imagine a large sheet of paper which is flexed in arbitrary ways. This represents an arbitrary open surface. Many of the curves we will draw will be confined to this surface, i.e. confined to the paper. Since the paper is bent, these curves are also bent in arbitrary ways in three-dimensional space even though they must remain on the paper. Thus, they are space curves, but for simplicity we will just call them curves.

We will frequently draw line segments to connect two arbitrary points on the surface as a measure of the minimum distance between the two points in three dimensional space. Thus, these line segments are not confined to the surface. Instead, they connect points on the surface across a bend or fold of the surface. These connecting line segments are called chords.

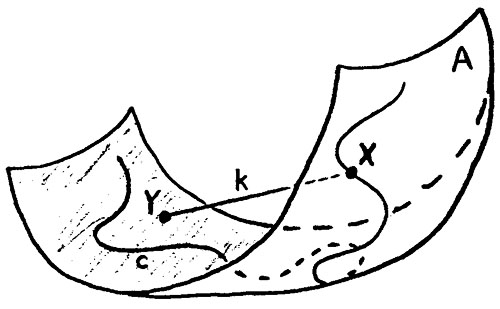
Figure 2 below illustrates these terms.

Figure 2

Start with the open surface A. Curve c is a space curve that is confined to surface A. Points X and Y are on surface A, and point X is also on curve c. Chord k connects points X and Y, and is not confined to surface A. The length of chord k is the minimum distance between points X and Y in three dimensions.

Projections

We will also make use of projections. Typically we will project a chord onto a plane, thus creating a new straight line segment with a different length and a different orientation from the original chord. Although the analogy is over simplified, imagine a straw suspended over a horizontal desktop with a bright light above it. The straw may be at any arbitrary orientation. It represents the original chord. The shadow of the straw on the desktop is the projection of the chord onto the horizontal plane.

Another type of projection we will use is the projection of a chord onto the vertical. In this case the resulting projection will be a straight line segment parallel to the vertical having its highest point at the same elevation as the highest point of the chord and its lowest point at the same elevation as the lowest point of the chord.

Note that in both types of projection the length of the resulting line segment is usually shorter, possibly equal to, but never longer, than the original chord we decided to project. Also in both types of projection the orientation of the resulting line segment is usually different from the orientation of the original chord. Note that when projecting onto the vertical, the resulting orientation is completely fixed. It must be vertical no matter what the orientation of the original chord. When projecting onto a plane such as the horizontal, the direction is constrained but not fixed. It must be horizontal, but its azimuth matches the orientation of the original chord.

Transformations, Loops, and Shrinking

We will also need to be able to move our points and curves around on the surface, remembering to always keep them confined to the surface. Moving a curve or point across the surface in such a way as to keep it on the surface is called a transformation. When we transform a curve along the surface, any chords and projections associated with that curve move along with it, even though these are not confined to the surface.

A loop is a special curve that is drawn on the surface so that it connects back with itself, i.e., it is closed. Loops divide the surface into two areas, one inside the loop and one outside the loop. Curves that are not closed are not loops. If it extends to the edges of an open surface, an open curve might also divide the surface into two areas, but these areas could not be characterized as being either inside or outside the curve. Finally, a loop does not cross itself. For example, a figure-8 shaped curve is not a single loop, but rather two loops which happen to touch at one point.

As with any point or curve, we can move or transform loops drawn on a surface. One special type of transformation for a loop is to make it get smaller and smaller. This type of transformation is called shrinking. Open curves cannot be shrunk. Closed curves, including loops, can be shrunk.

What happens to a loop on our sheet of paper when we shrink it? For a circular loop, the radius gets smaller and smaller until it goes to zero. The loop has shrunk to a point. In this example, we kept the shape of the loop the same, i.e., a circle, for simplicity sake. In general, however, it is not necessary to preserve the shape of the original loop. It is only necessary that the area interior to the loop decrease as the loop shrinks. All loops drawn on a flexed sheet of paper can be shrunk to a point, no matter how big or what shape they are originally. This is not true for all surfaces, however. On certain types of surfaces, some loops can only be shrunk so far. This important distinction is fundamental to the system of arch dimension definitions presented here. It is also key for defining what a natural arch is.

Holes and Orbits

In what follows, the term hole is used as it is defined in the mathematical discipline of topology. The surface of an arch, i.e., the surface that bounds the rock frame (and any fill material) from the air that surrounds it, has a topological hole. If we draw loops in various places on the arch surface, it will become apparent that some loops can be shrunk to a point while others cannot.

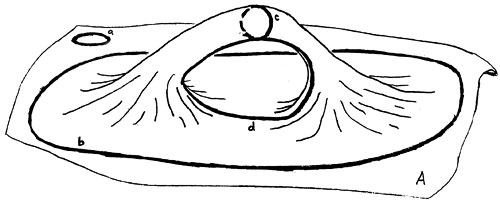
Figure 3 shows the four types of loops that occur on an open surface with a hole, i.e., an arch surface:

Figure 3: A is an open surface with a hole. It is the surface of a natural arch. Loop a is a point loop. It can be shrunk to a point. Loop b is a boundary loop. It can't be shrunk to a point because it surrounds the entire arch. Loop c can't be shrunk to a point because it encircles the lintel. It is called a lintel orbit. Loop d can't be shrunk to a point because it encircles the opening. It is called an opening orbit.

Loops which can be shrunk to a point are called point loops, e.g. loop a. Loops which cannot be shrunk to a point because they completely surround the arch are called boundary loops, e.g. loop b. Remember in shrinking the loop that all parts of it must remain on the surface at all times.

Some loops cannot be shrunk to a point because they either encircle the arch's lintel, e.g., loop c, or the arch's opening, e.g., loop d. (See Natural Arch Components for definitions of the opening and lintel.) Loops which encircle either the opening or the lintel are called orbits. Orbits around the opening are called opening orbits and orbits around the lintel are called lintel orbits. Orbits, chords associated with orbits, and projections of those chords are the basic building blocks used to define many of the standard set of natural arch dimensions.

An arbitrary orbit, while confined to the arch surface, is still free to wander anywhere on the surface, i.e., it can be transformed so that it contains any point on the surface. Orbits that are also restricted to a plane are a special subset of the general class of orbits. Such orbits are defined by the intersection of a plane with the surface and are called planar orbits. An example of a planar lintel orbit is depicted in Figure 4, which shows the intersection of a plane with the arch's lintel. One can also easily imagine a planar opening orbit defined by the intersection of a plane with the arch's opening.

Figure 4: Plane P intersects the arch surface through the lintel, thus defining a planar lintel orbit. If the plane happened to be vertical, it would define a vertical lintel orbit. Planar opening orbits are defined similarly, including vertical and horizontal opening orbits when they exist.

Planar orbits defined by planes that are vertical or horizontal form two other important subsets of orbits. These are called vertical orbits and horizontal orbits respectively, where the word planar is understood. Vertical lintel orbits, horizontal lintel orbits, vertical opening orbits, and horizontal opening orbits are also key ingredients of the definitions offered here.

Min/max Operator

One more key term remains to be defined in the set of basic mathematical terms used in the definitions, the min/max operator. This operator is somewhat complex and is best explained with an example.

Imagine a set of objects (for example apple trees in an orchard) each of which has a set of other objects (for example apples) associated with it. Furthermore, assume that each of these other objects exhibits a characteristic that is measurable (for example the diameter of an apple.) In this example of an apple orchard, we want to estimate the productivity of a specific tree. One of the numbers that will help estimate this is the diameter of the largest apple on the tree in question. After the diameters of all the apples on the tree are measured, we determine which diameter is the largest and then associate that value with the tree. In short, let the maximum apple diameter produced by tree N be designated as D_N.

Now we want to do some analysis on the productivity of the entire orchard. We want to quantify the minimum yield of any tree in the orchard. A number that will help estimate this is the smallest of all the maximum diameters, D_N. We first determine D_N for each tree and then determine the smallest of these values. This is the minimum D_N for the orchard. The smallest of the largest.

The term min/max is a convenient notation that represents the selection process described in the orchard example above. It selects the minimum value from a set of maximum values, each of which was previously selected from a set of some measurable quantity.

Now let's look at an example a little closer to our subject than apples and orchards. Consider a chord drawn between two arbitrary points on an orbit. The length of the chord measures the distance between the two points. Next, consider all possible chords that could be drawn between any two points on the orbit. There is obviously an infinite number of chords, but don't be daunted. Of all those possible chords, what chord is the longest, i.e., has the maximum length? Typically, we don't have to draw all the chords to determine which is the longest. In most cases it will be obvious. In a few cases, we might have to measure two or three chords to see which is really the longest. In some very special cases, e.g., a circular orbit, many chords will tie for being the longest, but it will still be easy to determine that maximum chord length.

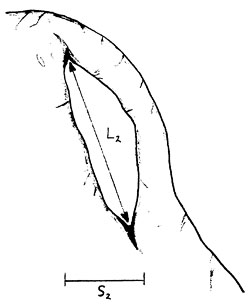
The maximum chord length we've just determined is a measure of the maximum spatial extent of the orbit we started with. Now let's examine a whole set of orbits which together form a surface. Consider the entire set of maximum chord lengths for every orbit on this surface. From this set of maximum chord lengths, select the shortest. We'll call this value the min/max of chord lengths for all orbits of the surface. This min/max of chord lengths, i.e., this shortest of the longest chords, is a measure of the spatial extent of our surface where it is most constrained. In fact, had we been dealing with opening orbits on an arch surface, the min/max of chord lengths would be the distance L in Figure 1 below. L is one of the standard dimensions of a natural arch.

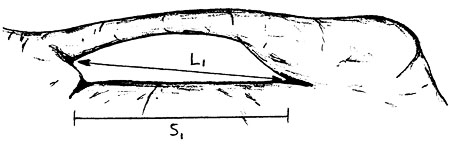
Figure 1a

Figure 1b