On Measuring Arches

by Jay H. Wilbur

Finding the Span of Arches with Simple Shapes

Introduction

I am frequently asked, "How do you measure the span of an arch?” Of course, those who ask expect a simple, straightforward answer. Unfortunately, for an arbitrarily shaped arch, the answer is anything but simple. When I try to give an answer for the general case, most people are sorry they asked. Eyes glaze over and the subject changes rapidly. On the other hand, if we’re at a specific arch, and I explain how to measure that particular arch, most people have no problem understanding.

The rigorous definitions for the dimensions of natural arches that were developed by the NABS Standards and Definitions Working Group (SDWG), and that are available on this website, do, in fact, cover the general case. However, they are also rather technical and may be hard to understand by those without a background in math. Much simpler explanations can be developed for arches with simple shapes.

In this article we will limit ourselves to discussing how to measure the span for arches whose two opening entrances are roughly parallel and relatively close together. For those familiar with the SDWG's standard attribute list, these are the five types of "apertures.” These five types of openings can be treated as if they were two-dimensional, i.e., in a single plane. This makes measuring them much easier. At least, it makes it much easier to determine what points on the surface of the arch to measure. Of course physically getting to those points with a measuring device may still be quite a problem.

Semicircular Apertures

Let’s start with the opening shape labeled as a semicircular aperture by the SDWG. Shelter natural arches and all but the youngest alcove natural arches have this type of opening. So do many meander natural bridges and abandoned, arc, and sea natural arches. Other types may also occasionally take on this shape. It is certainly one of the most common opening shapes found. That’s because it results from wall collapse, a very common process of arch formation. Other formation modes can also produce this shape.

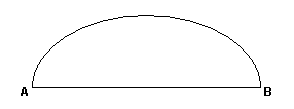
Semicircular apertures are always upright, i.e., the opening entrances are roughly vertical planes. The base of the arch, i.e., the bottom of the opening, is roughly horizontal. In the case of shelter natural arches, the base is a horizontal plane, i.e., a floor. For alcove natural arches, the base might also be a plane, or simply a line. In all cases, the underside of the lintel has taken on the shape of an inverted catenary, i.e., roughly a semicircle. If you drew a flat, two-dimensional picture of the opening, it would look something like Figure 1.

Figure 1

Of course, no real arch opening looks exactly like this highly idealized schematic. Any real natural arch will have plenty of irregular deviations from this ‘perfect’ shape. We will have to account for these ‘imperfections’ when measuring real arches, but let’s start by measuring the span of this idealized opening.

The technical definition of the span found on the NABS website is, "the min/max of the lengths of the horizontal projections of the chords of all opening orbits.” But we can greatly simplify this for semicircular apertures. Because we are able to consider this type of opening to be in a single plane, we need only consider one of its opening orbits. In fact, we don’t even need to use the term orbit. In this case, the technical definition simplifies to, ‘the maximum horizontal extent of the opening,’ where we are considering the opening to be in a single plane. In Figure 1, this is simply the distance between points A and B.

Now let’s add just a little more reality, that nasty third dimension. Even apertures are three-dimensional and care must be taken when reducing the problem to two dimensions. Examine Figure 2. This is also a highly schematic idealization of a semicircular aperture, but now the arch is depicted in 3-D. Some people might assume that the span is the largest distance under the lintel, i.e., the distance between points C and D. This dimension is actually known as the extent of the arch and was defined and used by Stevens and McCarrick in their book on Arches National Park (reference 2). However, the SDWG was unable to develop a rigorous definition for this dimension and did not include it in the standard set of measurements. Other people might assume that the span is the average distance under the lintel, i.e., the distance between points E and F, but this is also not the case. The span should be measured where the opening is most constrained, i.e., the distance between points A and B.

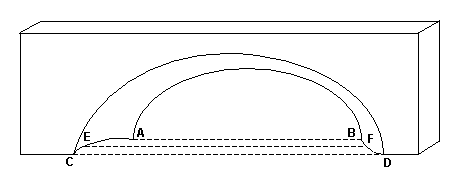
Figure 2

Before we consider those ‘imperfections’ we mentioned earlier, let’s digress to consider some techniques for actually measuring the distance between points A and B. If both points are accessible, and it is possible to move across the base of the arch, then stretching a steel tape between the two points is probably the easiest and most reliable way to take the measurement. I routinely carry a 50-foot steel tape for this purpose. Stretching a length of line or rope between the points and measuring this length later is also a common technique. If done carefully, these methods usually produce measurements with an accuracy of a foot or two.

Greater accuracy can be obtained by using laser-ranging equipment. The best technique is to place the ranging device at one of the points and directly measure the distance to the other. A technique that is often easier, and has only slightly less accuracy, is to range to points A and B from a point along the line that connects them, and then add these two ranges to get the total distance between A and B. Laser ranging, if done correctly, will yield measurements accurate to a few inches or even less.

Of course, if no other measuring equipment is available, the distance can be estimated by pacing it off. At home, measure the length of your maximum, minimum, and average strides. At the arch, pace off the distance three times. First count the number of maximum strides between the two points and multiply by your maximum stride length. Repeat using your minimum and average strides. A reasonably good estimate of the distance is the average of these three results. You can also get a rough estimate of the accuracy of the result by seeing how much the three measurements vary.

Of course, the bases of many arches are not accessible. Obviously for these arches, the direct measurement techniques described above won't work. However, two other techniques, triangulation and photo analysis, can be used to get reasonably accurate measurements of the span.

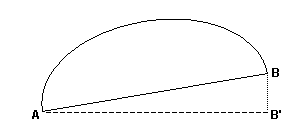
Now, let’s get back to those ‘imperfections’, and how to account for them. The first one we’ll consider is deviations from a true horizontal base. The definition of a semicircular aperture allows such a deviation, but the definition of the span does not. Thus, when measuring the span of a semicircular aperture that has a base tilted from the horizontal, we must make an adjustment. Consider the opening depicted in Figure 3. The base of the arch extends at an angle from point A to point B. In this case, the span is not the distance between points A and B. Rather it is the projection of that distance onto the horizontal, i.e., the distance between A and B'. This distance usually has to be calculated based on indirect measurements. For example, from measurements of the distance between A and B, and either the angle BAB' or the vertical distance between B and B', the span can be calculated using trigonometry.

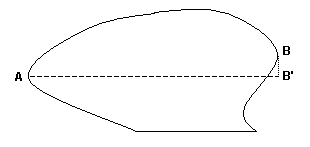
Figure 3

The other ‘imperfection’ frequently encountered is where one or both of the abutments have a notch or irregularity that extends the opening past the point where the abutment meets the base. Figure 4 depicts the worst case, where both abutments have such an extension, and the line connecting them is not horizontal. In this case, we must measure the distance between points A and B, and then calculate the projection of that distance onto the horizontal. This gives the span, i.e., the distance between A and B'.

Figure 4

Upright oval and slotted apertures

Next, we look at those openings with shapes labeled by the SDWG as an upright oval aperture or an upright slotted aperture. Fin natural arches have openings that are upright oval apertures. Buttress natural arches have openings that are either half-semicircular apertures or upright oval apertures. Propped natural arches have openings that are upright slotted apertures. Some abandoned, caprock, and sea natural arches have openings with these shapes as well.

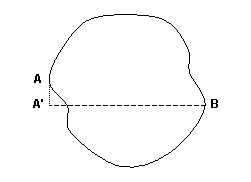
Figure 5

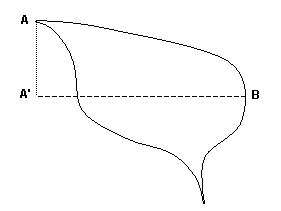
Figure 6

These openings have a lot in common with the semicircular apertures. They have entrances that are roughly vertical planes that are relatively close and roughly parallel. Here again, the opening can be considered to be in a single plane for purposes of measuring the span. Figure 5 shows a schematic drawing of a typical upright oval aperture. The span is the distance between A' and B. Figure 6 shows a schematic drawing of a typical upright slotted aperture. Again, the span is the distance between A' and B. Finding the span of such opening shapes is the same as for semicircular apertures. What we want to measure is the largest horizontal ‘footprint’ of the opening, where once again we consider only the plane of the opening where it is most constrained.

Prone oval and slotted apertures

Finally, we examine openings with shapes labeled by the SDWG as a prone oval aperture or a prone slotted aperture. Young alcove natural arches have openings that are prone slotted apertures. Some caprock, cave, and lava natural arches, and some waterfall natural bridges have openings that are either prone oval apertures or prone slotted apertures.

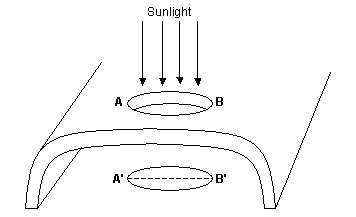
The two types of prone apertures (slotted and oval) have entrances that are roughly horizontal planes that are relatively close. They are similar to the upright apertures discussed above, except they are horizontal instead of vertical. Once again, we consider the opening to be in a single plane, now a horizontal plane. Finding the span of a prone aperture is the same whether it is slotted or oval. Again, similar to the other types of apertures, the span is the largest horizontal extent of the opening, considering the opening to be in a single plane, the plane where it is most constrained.

Imagine a horizontal plane beneath the aperture, i.e., a floor under the arch, and imagine the sun shining down on the arch from directly above. The bright patch of light on the horizontal plane is the projection of the opening onto the horizontal. The width of this patch at its widest is the same length as the span of the arch. This is depicted in Figure 7. Indeed, when the base of the arch actually is a horizontal plane (which is true for many cave natural arches and some other types as well) and the sun is directly overhead, measuring the light patch on the floor with a steel tape is an easy and practical way to estimate the span of the arch. Watch out though. If the sun is at an angle, the light patch will be distorted and you might get spurious results.

Figure 7